1.
The amount at a later point in time is known as a
future value.
2.
Compound (or Compounded) interest refers to earning interest on previously earned interest.
3.
The amounts contained in a future value of 1 table for various combinations of n and i are referred to as future value
factors.
4.
In the future value of 1 table, n refers to the number of
periods of time, such as months, quarters, years.
5.
If you know the future value of a single deposit, the interest rate, and the number of periods that the interest is compounded, you will be able to calculate the
present value by using a future value of 1 table.
6.
Assume that you are calculating the future value of a single deposit by using a future value of 1 table. The deposit will be invested in an account earning 12% per year for four years. If the interest will be compounded quarterly, the number of periods (n) will be
16 (4 years X 4 quarters per year) and i will be 3%.
7.
An unrestricted deposit of $1,000 grows to a future value of $5,000 through the compounding of interest. Under the accrual basis of accounting, the $4,000 of growth should be reported as
interest revenue (or interest income).
8.
Under the accrual basis of accounting, the interest earned over a three-year period on a single deposit should be reported on a company's income statement .
9.
Which compounding of an 8% annual interest rate will result in a larger future value?
10.
If you know the present value of a single amount, the future value of that amount, and the number of periods that the interest will be compounded, you can calculate the
interest rate.
11.
When using the future value of 1 table to calculate the future value of a deposit earning 10% per year compounded semiannually, you would use a factor from the column headed
5% (10% per year divided by 2 six-month periods per year).
12.
An account or deposit will earn 12% interest per year for two years. Assuming that you are using the future value of 1 table and the interest is compounded monthly, you will find the factor in the row where n is
24 (2 years X 12 months per year) periods.
13.
An account or deposit will earn 12% interest per year for two years. Assuming that you are using the future value of 1 table and that the interest is compounded monthly, you will find the factor in the column where i is
1% (12% divided by 12 months per year).
Use the following future value of 1 factors for solving the remaining questions:
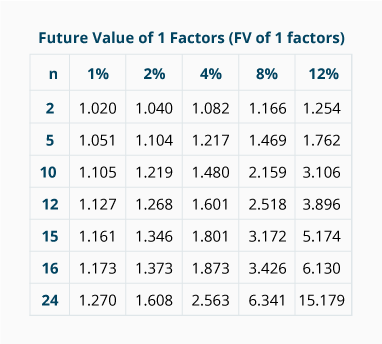
14.
A deposit of $1,000 on January 1, 2025 will have a future value of $
$1,469.
FV of 1 = PV x FV of 1 factor for n = 5 years, i = 8% compounded annually
FV of 1 = $1,000 x 1.469
FV of 1 = $1, 469 on December 31, 2029 (or January 1, 2030) if it is invested at 8% per year and the interest is compounded annually.
15.
A deposit of $10,000 on January 1, 2025 will have a future value of $
$14,800.
FV of 1 = PV x FV of 1 factor for n = 10 semiannual periods, i = 4% per semiannual period
FV of 1 = $10,000 x 1.480
FV of 1 = $14,800 on December 31, 2029 (or January 1, 2030) if it is invested at 8% per year and the interest is compounded semiannually.
16.
A deposit of $2,000 on January 1, 2025 will have a future value of $
$2,540.
FV of 1 = PV x FV of 1 factor for n = 24 months, i = 1% per month
FV of 1 = $2,000 x 1.270
FV of 1 = $2,540 on December 31, 2026 (or January 1, 2027) if it is invested at 12% per year and the interest is compounded monthly.
17.
A deposit of $1,000 on January 1, 2025 will have a future value of $
$1,373.
FV of 1 = PV x FV of 1 factor for n = 16 quarters, i = 2% per quarter
FV of 1 = $1,000 x 1.373
FV of 1 = $1,373 on December 31, 2028 (or January 1, 2029) if it is invested at 8% per year and the interest is compounded quarterly.
18.
The interest rate that is necessary for a deposit of $1,000 to grow to $5,474 after 15 years of interest compounded annually is
12%.
FV of 1 = PV x FV of 1 factor for n = 15 years, i = ??% compounded yearly;
$5,474 = $1,000 x FV of 1 factor for n = 15 yrs, i = ??% compounded yearly;
5.474 = FV of 1 factor for n = 15 yrs, i = ??% compounded yearly;
Look only in the row, n = 15, and locate the factor 5.474. It is in the column where i = 12%.% per year.
19.
The annual interest rate that is necessary for a deposit of $1,000 to grow to $1,373 after four years of interest compounded quarterly is
8%.
FV of 1 = PV x FV of 1 factor for n = 16 quarters, i = ??% per quarter;
$1,373 = $1,000 x FV of 1 factor for n = 16 qtrs, i = ??% per quarter;
1.373 = FV of 1 factor for n = 16 qtrs, i = ??% per quarter;
Look only in the row, n = 16, and locate the factor 1.373. It is in the column where i = 2%. This means that the rate per quarter is 2%. Since the question is asking for the annual rate, multiply the rate per quarter times 4 to arrive at 8% per year.% per year.
20.
The number of years required for an investment of $1,000 to grow to $2,563 when invested at an annual rate of 8% compounded semiannually is
12 years.
FV of 1 = PV x FV of 1 factor for n = ?? six-month periods, i = 4% semiannually;
$2,563 = $1,000 x FV of 1 factor for n = ?? six-month periods, i = 4% semiannually;
2.563 = FV of 1 factor for n = ?? six-month periods, i = 4% semiannually;
Look only in the column, i = 4%, and locate the factor 2.563. It is in the row where n = 24. This means that the number of six-month periods is 24, and that equals 12 years. years.
